From our last lesson, we know that we can use a linear basis function regression
\[\hat{y_i} = w_0 \phi_0(x_i) + \cdots + w_p \phi_p(x_i) \]
to fit a polynomial model
\[\hat{y_i} = w_0 + w_1 x_i^1 + \cdots + w_d x_i^d \]
of degree \(d\). We can then use ordinary least squares to find optimal values for the parameters \(w_0, \ldots, w_d\).
In retrospect, the course of the COVID-19 pandemic in late spring and summer of 2020 is known. In Spring 2020, however, with the rest of the spring and summer still to come, a number of models were developed to predict the extent of COVID-19 deaths over the coming weeks. Most of these models tried to simulate the epidemiological processes involved in the spread of disease, under various conditions and assumptions (e.g. different levels of restrictions on mobility and other non-pharmaceutical interventions). The predictions of these models varied widely according to their assumptions.
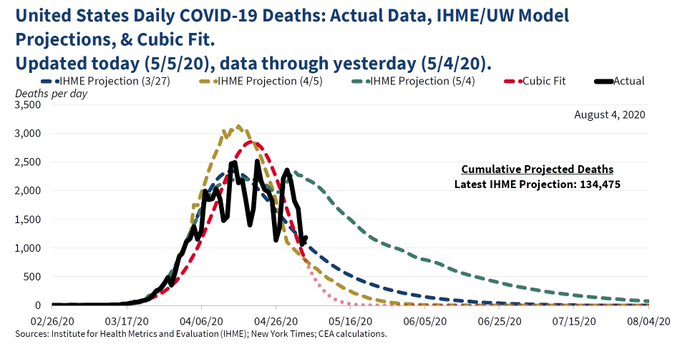
There was one model in particular that seemed to suggest the pandemic would come to an end very soon. In May 2020, an article in the Washington Post revealed the existence of the “cubic model”:
Even more optimistic than that [a different model], however, is the “cubic model” prepared by Trump adviser and economist Kevin Hassett. People with knowledge of that model say it shows deaths dropping precipitously in May — and essentially going to zero by May 15.

This “cubic model” attracted some attention, because it predicted fewer deaths than other models. Also, many individuals pointed out that the “cubic model” looked like someone had just fit a polynomial model to the available data, without any consideration of whether epidemiology or infectious disease dynamics supported the use of such a model.
Shortly after this, the Council of Economic Advisors clarified that the model was indeed “just a canned function in Excel, a cubic polynomial.” However, they said that this “cubic model” was for data visualization purposes only; it was never intended to be a projection of future deaths. Another member of the adminstration told CNN that “we didn’t change anything based on that,” i.e. the “cubic model” was not used to inform any U.S. policy.
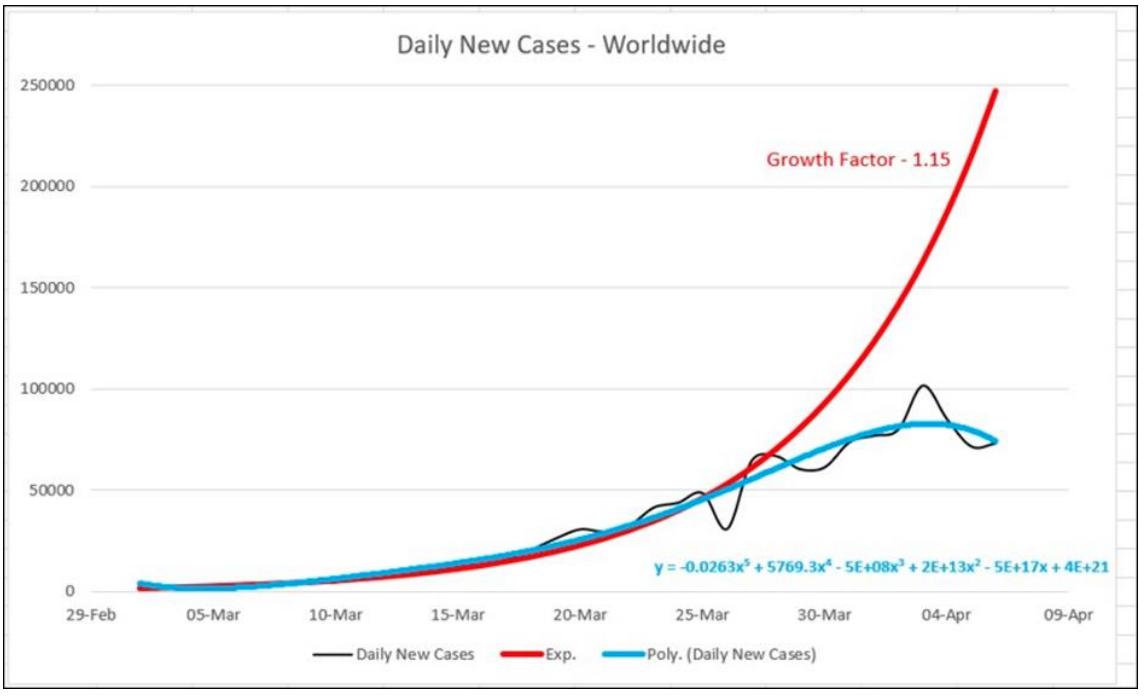
Even if the Council of Economic Advisors hadn’t intended for the cubic model shown above to be used as a forecast, others around the world were also fitting polynomial models to COVID-19 data, and claiming that their models had predictive value. In Israel, Isaac Ben-Israel, a professor at Tel Aviv University (and also chairman of the Israeli Space Agency and of Israel’s National Council for Research and Development), similarly claimed that cases would go to zero in May 2020. In the report he produced to support his claims, he cited models like the following, based on a fitted polynomial of degree 6:
Similarly, Times Now News in India produced a set of models to forecast COVID-19 conditions in India, including a polynomial model of degree 2 and a polynomial of degree 3, with a claimed “average forecasting accuracy of over 94% & 98% respectively”.
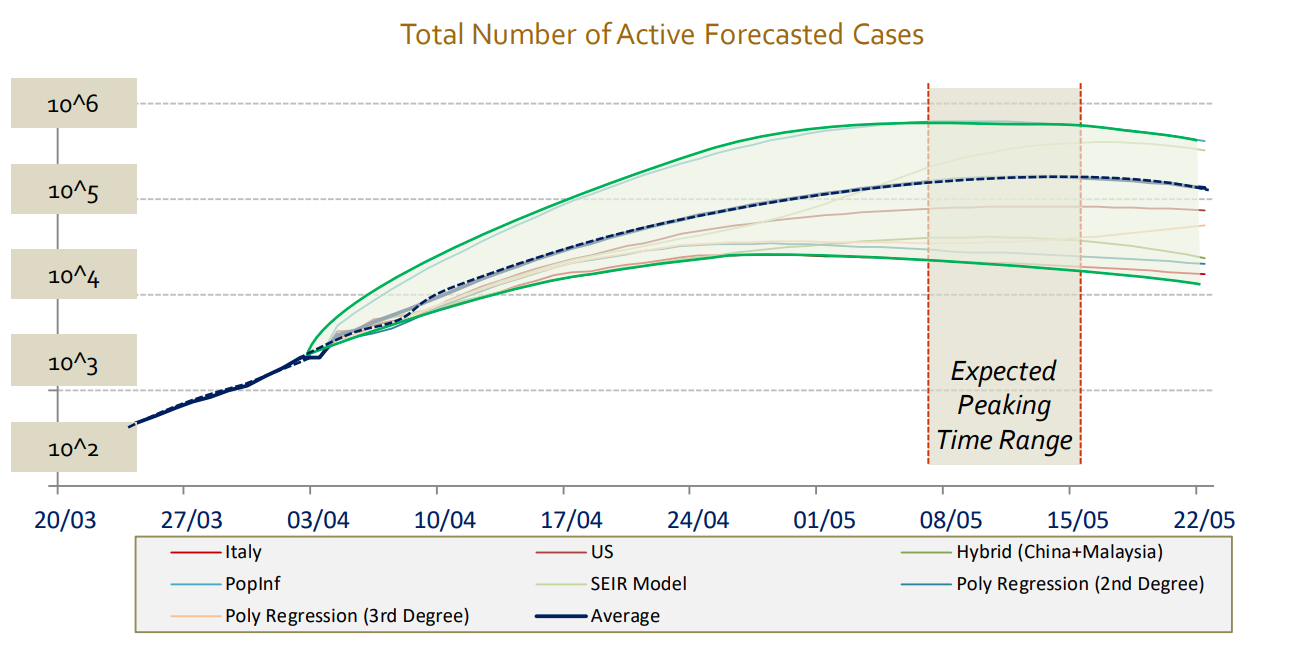
The forecasts produced by these models were all very wrong, but they appeared to fit the data well! What was wrong with the approach used to produce these models? How did they miscalculate so badly?